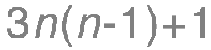Artwork Allusions

Incredible String Band

Allusions in the artwork. Particularly referring to the Incredible String Band, for whom BoC have a great deal of respect, and whom they apparently see from time to time. The lyrics section reveals that they have sampled the ISB occasionally; there's the old track "ithcus sound", a possible reference to the ISB track "ithkos". There's a general similarity in mood between Geogaddi and such ISB songs as "Waltz of the new moon" (HBD). It has also been observed that the title "Geogaddi" might in part refer to the ISB song "koeeaddi there" (HBD again).

One interviewer comments that the front covers of the ISB's "The Hangman's Beautiful Daughter" and BoC's "Music Has The Right To Children" would make "a nice pair":

• 
• 

However, but there is a far more striking similarity between the back cover of the ISB album, and some of the pictures of BoC available elsewhere; if this is any more than coincidence, and it may be no more than that, it makes a nice tribute to the ISB:

• 
• 

The next pair aren't all that similar, except in their mood, but here they are anyway:

• 
• 

Geogaddi Cover

[Roger B] has pointed out something about the cover art of the Geogaddi album: In the scene in the film "The Wicker Man" that features dancing around a maypole, a figure is seen in silhouette (by his shadow on the grass). The pose is very similar to that in the picture used to make the album cover. (Thanks, Roger). Below, is a frame from that film. To the right, the photo on which the Geogaddi cover is based (the picture was taken by Peter Iain Campbell, as is noted on the back of the album).

• 
• 

However, [Tonamel Rhysthal] has another suggestion, that the pose mirrors that of Leonardo da Vinci's famous "Vitruvian Man". Wikipedia, always a good resource, has an article on Vitruvian Man. The link between this figure and the relation between art and mathematics fits in very well with some of the other images BoC had on their site (see below), and also with one of the themes of Geogaddi (religious iconography and geometry).

My Bloody Valentine

The following information has been given by [7seals]. The front covers of both albums. Note the very similar font used (Bauhaus). Faces obscured. (in Music Has the Right to Children, it seems artificial whereas in isn't anything it seems to be intentionally caused by overexposure).

• The front covers.
• 
• 

• The inside front covers.
• 
• 

• The inserts.
• 
• 

• The back covers of the albums.
• 
• 

The Campfire Headphase

[Khov] made a post on the watmm forum about one of the small artwork pictures on The Campfire Headphase cover which obviously has been taken from [this 1979 yearbook picture].

• 
• 

Trans Canada Highway Cover

[Damien] made a post on the old guestbook about the striking resemblance between the Trans Canada Highway cover and a 1977 Dodge operation manual. No coincidence.

• 
• 

Various

[DC] stumbled across this purely by accident: one of the little images in the artwork of the In a Beautiful Place out in the Country single comes from here (where the image is explained).

Numbers & Patterns

Pascal's Triangle

An older version of the BoC website briefly had some black-and-white drawings on a page, which contained Pascal's Triangle. Alas, the page at web.archive.org is dead.

Some of the pictures that were accessible on that page (and reproduced below) have interesting references that might not be apparent at first glance. Putting his interest in mathematics to use, [DC] submitted the following section about the images; he adds that, while he is interested in maths, and the mathematical patterns to be found in nature, he does not personally believe in the merits of numerology. As former maintainer of this site, he requests that that section, below, be left just as it is as his own lasting personal contribution to the site.

Firstly, there's Pascal's Triangle itself. Each number is the sum of the two diagonally above it. If you start at the top and follow it down diagonally:

• the first column consists only of 1's (a single zero-dimensional point),
• the next has the positive integers 1,2,3,.... (dots arranged in a 1D line),
• then triangular numbers: 1,3,6,10,15,21,... (dots arranged in 2D triangles),
• then the tetrahedral/pyramidal numbers : 1,4,10,20,35,56... (dots arranged in 3D tetrahedrons);
• then: 1,5,15,35,70,126... (dots arranged in 4D '4-simplex' arrangements);

and so in, into ever higher-dimensional analogues of the triangle.

Another example - tossing coins: take the row "1,4,6,4,1". If you toss a coin 4 times, the chances of getting 0,1,2,3, and 4 heads (or tails) are, respectively: 1/16, 4/16, 6/16, 4/16, 1/16. If you toss it 5 times, the chances of 0,1,2,3,4,5 heads (or tails) are: 1/32, 5/32, 10/32, 10/32, 5/32, 1/32 (from the next row). And so on.

The total of the numbers in each row is a power of two. There are many more relations - a whole page could be devoted to Pascal's Triangle alone - but I'll let readers pursue this themselves. There's a Dr Math article on it, and another site devoted to Pascal's Triangle even explains how you can get the Fibonacci numbers from it, among other things.

Various Math Related Pictures

A visual illustration depicting a facet of Einstein's theory of relativity.

---

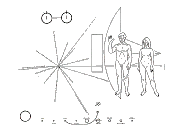
The Pioneer 10 plaque: it shows the location of the earth relative to distant pulsars (lower-left of picture), and the height of the woman relative to the space-craft. The two spheres beside each other (top-left) represent the reversal of spin of an electron in a hydrogen atom, which results in the emission of 21cm radio waves. Therefore, all distances on the plaque are indicated in terms of 21cm units.

---

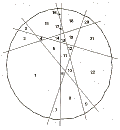
A demonstration that the maximum number of regions into which you can divide a plane using 6 lines is 22.

---

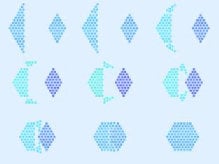
The formula 3n(n-1)+1. This gives the sequence 1, 7, 19, 37, 61, 91, .... These are the centered hexagonal numbers. The nth centered hexagonal number is 1 more than 6 times the (n-1)th triangular number. You can make a series of hexagons of different sizes using coins (or indeed small hexagons). The first degenerate case is a single coin = 1. You can place six more coins around this one to make a hexagon with 7 coins. You can place twelve more coins around the outside of this hexagon to make a larger hexagon with 19 coins. And so on, adding another eighteen to get 37, then another twenty-four to get 61. My own illustration of this is below.

Whereas centered hexagonal numbers make filled-in hexagons, the "cornered" hexagonal numbers {1, 6, 15, 28, 45, ...} make the outlines of hexagons. They are given by the formula n(2n-1), or every other triangular number (starting with 1 which is by convention the zeroth). The centered and cornered hexagonal numbers are related by the following formula. Let x be the nth centered hexagonal number and y be the nth cornered. Then x = y + n²

---

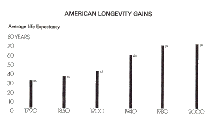
A graph of changes in life expectancy.

---

Possibly, a poem by the Saucepan Man from an Enid Blyton book - from the "Magic Faraway Tree" series of books, I think!

---

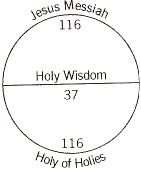
Presumably making the point that the ratio of the gematria for "Jesus Messiah" and "Holy Wisdom" in Hebrew, namely 116/37 or 3 + 5/37, is a good approximation to π.

---

The Greek Sphinx was said to have "the bust and head of a lady, the wings of an eagle, the body and legs of a lioness, and the tail of a snake or dragon".

---

A pyramid or triangle of 703 dots made up of 296 dots on top, and a further 407 dots below. The Hebrew words in the picture are the last two words of Genesis 1:1, namely, the word for "and", and the word for "the earth" (Hebrew is written from right to left). The gematria for the words for "and" and "the earth" are 407 and 296, respectively (400+1+6, and 90+200+1+5; for further details on gematria, you can do your own research). The total for these two words is 407 + 296 = 703. As it happens, 703 is a triangular number, meaning simply that 703 dots form a triangle, as shown in the image. Triangular numbers can be expressed in the form 1+2+3+...+n-1. 703 is the 38th triangular number, 1+2+...+37 = 703. The number 38 is the sum of the rows of the magic hexagon; this sum is known as a magic constant.

Triangular numbers have the general formula n(n-1)/2. E.g. the 37th triangular number is 37×36÷2 = 666. Combinatorially, the triangular numbers are the "choose-two" numbers because they count the number of ways to pick 2 objects from a set of N objects (not counting the order by which you pick them).

37 crops up a lot here. Note that 407, 296, and 703 are all divisible by 37. Also note that if, against convention, you were to count 1 as being the first triangular (instead of the zeroth), then 703 would be the 37th triangular number.

---

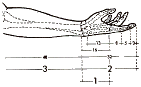
Anatomical diagram with many Fibonacci numbers, powers of two, and so on. Perhaps relates to the work of medieval artists, relating ideal proportions of the body in art to the Golden Section, and so forth.

---

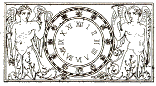
A clockface flanked by angelic figures. Perhaps taken from the frontispiece of a book.

---

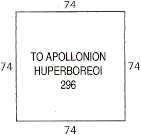
A square, with a dedication to the "Hyperborean Apollo" (in transliterated Greek, which I find more confusing to read than Greek itself, since I expect the letters to have their Greek values). Pythagoras was regarded by some as the incarnation of the Hyperborean Apollo. 296, the figure in the box, is four times 74, the figure at each edge. Pythagoras and his followers: saw a connection between music and mathematics, and discovered that notes in the scale were connected by mathematical ratios. For example, the ratio of the frequencies of two notes separated by a major third (e.g C and E) are 5/4. For a fourth (e.g. C and F), it is 4/3, and for a fifth (e.g. C and G), it is 3/2. Of course, they were quite correct about the mathematical underpinnings of harmony - see Jean-Philippe Rameau's classic text, "A Treatise on Harmony". In that sense, music is, indeed, math.

---

An unrelated point I noticed when thinking about hexagonal numbers: a BoC track is called "Triangles and Rhombuses". You can make each hexagonal number from a triangular number plus a square (which can be drawn as a rhombus).I don't know whether BoC had this in mind when they named the track, but I just mention this for interest anyway. Examples of "triangular number" + + square" = "hexagonal number"

0 + 1 = 1, 3 + 4 = 7, 10 + 9 = 19, 21 + 16 = 37, 36 + 25 = 61, and so on.

If you want to work it out for yourself, use: Triangle(n) = n(n+1)/2 ♦ Rhombus(n) = n2 ♦ Hexagon(n) = 3n(n+1)-1 and show that: Triangle(2n-2) + Rhombus(n) = Hexagon(n)

Here's a picture, using some frames from one of my own animation sequences, to show how this works, geometrically: